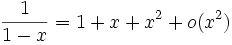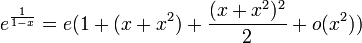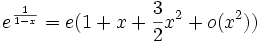Les développements limités

Publié le 15 janvier 2011 par Mathenigme

Somme :
: Si ƒ et g possèdent deux D.L._n, alors ƒ + g possède un D.L._n qui s'obtient en effectuant la somme des deux polynômes.

Multiplication par un scalaire :

: si ƒ possède un D.L._n alors λ·ƒ aussi, obtenu en multipliant le D.L._n de ƒ par λ.

Produit :

: Si ƒ et g possèdent des D.L._n, alors ƒ·g possède un D.L._n. Si a_k, b_k et c_k sont les coefficients de x^k dans les développements respectifs de ƒ, g et ƒ·g, le coefficient c_k est obtenu par la formule suivante :; $c_k = \sum_{i+j=k}a_ib_j\,$

Inverse :: Si u(x₀) = 0 et si u possède un D.L._n au voisinage de x₀, alors; $\frac{1}{1 - u}$; possède un D.L._n. Ce développement limité se trouve en cherchant un D.L._n de; $\sum_{k=0}^n u^k$

Composition :

si u possède un D.L._n au voisinage de x₀ et si v possède un D.L._n au voisinage de u(x₀), alors v o u possède un D.L._n au voisinage de x₀ qui s'obtient en cherchant un D.L._n de Q_n o P_n où P_n et Q_n sont les D.L._n de u et v

ex : développement limité d'ordre 2 au voisinage de 0 de $e^{\frac{1}{1-x}}$

D.L.₂au voisinage de 1 de

e x

$e^x = e(1 + (x - 1) + \frac{(x - 1)^2}{2} + o((x - 1)^2))$

rem: le D.L. au voisinage de 1 de $e x$ se trouve en remarquant que $e x = e . e x - 1$ et en utilisant le D.L. de $e h$ au voisinage de 0

D.L.₂ au voisinage de 0 de

$\frac{1}{1-x}$

est

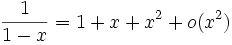
$\frac{1}{1-x} = 1 + x +x^2 + o(x^2)$

D.L.₂ au voisinage de 0 de $e^{\frac{1}{1-x}}$ :

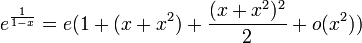
$e^{\frac{1}{1-x}} = e(1 + (x + x^2)+ \frac{( x +x^2)^2}{2} + o(x^2))$

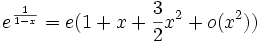
$e^{\frac{1}{1-x}} = e(1 + x +\frac{3}{2} x^2 + o(x^2))$

Intégration :

: Si ƒ est continue sur un intervalle I autour de x₀ et possède un D.L._n au voisinage de x₀, alors toute primitive F de ƒ possède un D.L._n+1 au voisinage de x₀ qui est; $F(x) = F(x_0) + \sum_{i=0}^{n}\frac{a_i}{i+1}(x - x_0)^{i+1}$

Dérivation :

il n'existe pas de théorème général sur l'existence d'un D.L._{n - 1} pour la dérivée d'une fonction admettant un D.L._n au voisinage de x₀.

par exemple la fonction définie par

$f(x) = x^3\sin\left(\frac{1}{x^2}\right)$

pour tout x non nul et ƒ(0) = 0

possède un développement limité d'ordre 2 au voisinage de 0 mais sa dérivée, non continue, ne possède pas de D.L.₁ .

Par contre si f' admet un D.L. d'ordre n-1 en x_o alors la partie régulière du D.L. de f' est la dérivée de la partie régulière du D.L. d'ordre n de f en x_o .